2269. Connected components
An undirected unweighted graph is given. Find the number of
its connected components.
Input. The first line contains
the number of vertices n (n ≤ 100). Then follow n lines
with n numbers each – the adjacency matrix of the graph. In the i-th
row, at the j-th position there is 1 if
vertices i and j are connected by an edge,
and 0 otherwise. The main diagonal of the matrix contains zeros. The
matrix is symmetric with respect to the main diagonal.
Output. Print one integer – the
number of connected components of the given graph.
|
Sample
input |
Sample
output |
60 1 1 0 0 01 0 1 0 0 01 1 0 0 0 00 0 0 0 1 00 0 0 1 0 0
0 0 0 0 0 0 |
3 |
SOLUTION
graphs – connected
components
Algorithm analysis
To find the number of connected components
in a graph, a disjoint-set data structure (Union-Find) can be used.
Initially, each vertex is placed in its own
set, and each vertex is the representative of that set. Then, for each edge (u,
v), the sets containing vertices u and v are united. After
processing all edges, the number of connected components equals the number of
sets in the structure.
This problem can also be solved using
depth-first search. In this case, the number of times the dfs procedure
is called will equal the number of connected components in the graph.
Example
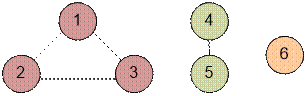
The graph given in the example looks as follows:
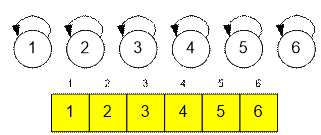
Initially, each vertex is placed in its own set, where it acts as the
representative.
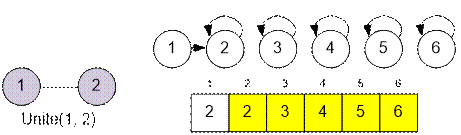
Then, for each
edge (u, v), the sets containing vertices u and v are united.
After processing all edges, two vertices will belong to the same connected
component if they have the same representative.
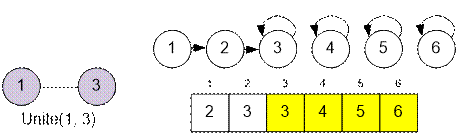
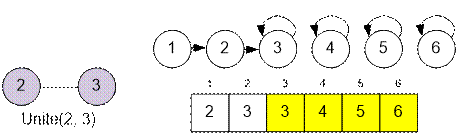
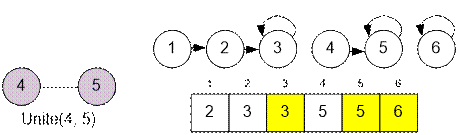
The number of
connected components is equal to the number of sets in the disjoint-set
structure. This number is determined by the representatives – those vertices v
for which the condition parent[v] = v holds.
In the given
example, the representatives are vertices 3, 5, and 6. Therefore, the graph
contains three connected components.
Algorithm implementation
MAX stores the maximum
number of vertices in the graph. In the array mas[i], the number of the
vertex to which vertex i points is stored.
#define MAX 102
int mas[MAX];
The function Repr returns the
representative vertex of the set to which vertex n belongs. To do this,
we follow the pointers sequentially until we reach the representative of the
set (a vertex whose pointer points to itself).
int Repr(int
n)
{
while (n !=
mas[n]) n = mas[n];
return
n;
}
The Union function merges two sets
containing vertices x and y. First, their representatives are
found – let them be x1 and y1. If x1 = y1, then the vertices already belong to
the same set, and no further action is required. Otherwise, the pointer of the
representative x1 is redirected to y1.
void Union(int
x,int y)
{
int x1 =
Repr(x),y1 = Repr(y);
if (x1 == y1)
return;
mas[x1] = y1;
}
The main part of the program. Each vertex initially points
to itself (mas[i] = i).
scanf("%d",&n);
for (i = 1; i <=
n; i++) mas[i] = i;
Read
the adjacency matrix. For each edge (i, j) where i < j,
perform a union of the sets containing vertices i and j.
for (i = 1; i <=
n; i++)
for (j = 1; j <=
n; j++)
{
scanf("%d",&value);
if (i > j)
continue;
if (value)
Union(i,j);
}
The variable count stores the number of connected
components. This number is equal to the number of representative vertices of
the sets – that is, those vertices that point to themselves.
count = 0;
for (i = 1; i <=
n; i++)
if (mas[i] ==
i) count++;
Print the answer.
printf("%d\n",count);
Algorithm implementation – depth
first search
Declare the arrays.
#define MAX 102
int g[MAX][MAX], used[MAX];
The dfs function performs a depth-first search
of the graph, starting from vertex v.
void dfs(int v)
{
used[v] = 1;
for (int i = 0; i < n; i++)
if (g[v][i]
&& !used[i]) dfs(i);
}
The main part of the program. Read the input data.
scanf("%d",&n);
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
scanf("%d",&g[i][j]);
The variable res stores the number of connected
components.
res = 0;
A depth-first search is performed on the disconnected
graph. Each call to the dfs function starts from an unvisited
vertex, so the number of dfs calls equals the number of connected
components in the graph.
memset(used,0,sizeof(used));
for (i = 0; i < n; i++)
if (!used[i])
{
dfs(i);
res++;
}
Print the answer.
printf("%d\n",res);
Java implementation – dfs
import java.util.*;
public class Main
{
static int g[][],
used[];
static int n;
static void dfs(int v)
{
used[v] =
1;
for(int i = 1;
i <= n; i++)
if (g[v][i] ==
1 && used[i] ==
0) dfs(i);
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
g = new int[n+1][n+1];
used = new int[n+1];
for(int i = 1;
i <= n; i++)
for(int j = 1;
j <= n; j++)
g[i][j] = con.nextInt();;
int res = 0;
for(int i = 1;
i <= n; i++)
if (used[i] ==
0)
{
dfs(i);
res++;
}
System.out.println(res);
con.close();
}
}
Java implementation – dsu
import java.util.*;
public class Main
{
static int mas[];
static int n;
static int
Repr(int n)
{
while (n != mas[n]) n = mas[n];
return n;
}
static void
Union(int x,int y)
{
int x1 = Repr(x);
int y1 = Repr(y);
if (x1 == y1) return;
mas[x1] = y1;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
mas = new int[n+1];
for(int i = 1;
i <= n; i++) mas[i] = i;
for(int i = 1;
i <= n; i++)
for(int j = 1;
j <= n; j++)
{
int val = con.nextInt();
if (i >
j) continue;
if (val ==
1) Union(i,j);
}
int count = 0;
for(int i = 1;
i <= n; i++)
if (mas[i] == i) count++;
System.out.println(count);
con.close();
}
}
Python implementation – dsu
The function Repr returns the
representative vertex of the set to which vertex n belongs. To do this,
we follow the pointers sequentially until we reach the representative of the
set (a vertex whose pointer points to itself).
def Repr(n):
while (n !=
mas[n]): n = mas[n]
return n
The Union function merges two sets
containing vertices x and y. First, their representatives are
found – let them be x1 and y1. If x1 = y1, then the vertices already belong to
the same set, and no further action is required. Otherwise, the pointer of the
representative x1 is redirected to y1.
def Union(x, y):
x1
= Repr(x)
y1
= Repr(y)
if (x1 == y1): return
mas[x1] = y1
The main part of the program. Each vertex initially points
to itself (mas[i] = i).
n = int(input())
mas = [int(i) for i in range (n + 1)]
Read
the adjacency matrix. For each edge (i, j) where i < j,
perform a union of the sets containing vertices i and j.
for i in range(1,n + 1):
lst = [0] + [int(j) for j in input().split()]
for j in range(1, n + 1):
if (i < j and lst[j] == 1): Union(i, j)
The variable res stores the number of connected
components. This number is equal to the number of representative vertices of
the sets – that is, those vertices that point to themselves.
res = 0
for i in range(1, n + 1):
if (mas[i] == i):
res += 1
Print the answer.
print(res)
Python implementation – dfs
The dfs function performs a depth-first search
of the graph, starting from vertex v.
def dfs(v):
used[v] = 1
for i in range(n):
if g[v][i] and not used[i]:
dfs(i)
The main part of the program. Read the input data.
n = int(input())
g = [[0] * n for
_ in range(n)]
used = [0] * n
for i in range(n):
row = list(map(int, input().split()))
for j in range(n):
g[i][j] = row[j]
The variable res stores the number of connected
components.
res = 0
A depth-first search is performed on the disconnected
graph. Each call to the dfs function starts from an unvisited
vertex, so the number of dfs calls equals the number of connected
components in the graph.
for i in range(n):
if not used[i]:
dfs(i)
res += 1
Print the answer.
print(res)